MATEMÁTICAS

ESTADÍSTICA

Es la ciencia que se encarga de diseñar, recolectar y analizar información para encontrar las principales características de un grupo de individuos a partir de una o mas variables.

Existen varias clases de estadísticas: la que vamos a estudiar se llama ESTADÍSTICA DESCRIPTIVA.

Estadística Descriptiva

La estadística descriptiva es la rama de las matemáticas  que describe el comportamiento de un hecho a través de la recolección, ordenamiento, clasificación y representación mediante cuadros, (por ejemplo, edad de una población, altura de los estudiantes de una escuela, etc.) y su finalidad es la de describir apropiadamente las diversas características de ese conjunto.

Ahora veamos algunos conceptos fundamentales para hacer un estudio estadístico:

Población	Es el grupo total de individuos motivo del estudio
Muestra	Es una parte de la población sobre las cuales se toma la información para analizar
Variable	Es una pregunta hecha para estudiar una característica de la población. La pregunta se debe hacer de tal forma que las respuestas correspondan a una escala numérica o se puedan contar. Para caracterizar una variable se tiene en cuenta 3 aspectos fundamentales, las tablas, las gráficas, y el análisis.

¿QUÉ ES UNA TABLA DE FRECUENCIAS?
Una tabla de frecuencias es un resumen de los datos en la cual se agrupan las respuestas a la variable teniendo en cuenta las respuestas.
Que columnas debe tener la Tabla de Frecuencias:	·      En la primera columna se ordenan las variables. ·      En la segunda columna se escribe Frecuencia Absoluta. ·      En la tercera columna la Frecuencia Absoluta Acumulada. ·      En la cuarta columna la Frecuencia Relativa ·  En la quinta columna la Frecuencia Relativa Acumulada.
Frecuencia Absoluta (f)	Es el número de veces que se repite un dato o una característica.
Frecuencia Absoluta  Acumulada (F)	Se obtiene escribiendo la primera frecuencia absoluta y a continuación se procede a sumar una a una las siguientes frecuencias absolutas obtenidas.
Frecuencia relativa (Fr)	Es el resultado de dividir la frecuencia absoluta y dividirla entre el número total de datos:  Se puede representar de tres formas: ·      Como fracción:  8/20 ·      Como un número:  0,4 ·      Cómo un porcentaje:  40%
Frecuencia relativa Acumulada	Es la frecuencia absoluta acumulada dividida por el número total de sujetos “n”

¿QUÉ SON LAS MEDIDAS DE TENDENCIA CENTRAL?
Son medidas estadísticas que pretenden resumir en un solo valor a un conjunto de valores. Representan un centro en torno al cual se encuentra ubicado el conjunto de los datos. Las medidas de tendencia central más utilizadas son: media, mediana y moda.
Media Aritmética o Promedio	Representa el valor hacia donde tienden todos los datos. Se halla al sumar todos los datos y dividirlos por el número total de ellos.  Su sigla es  Ma  o :
Mediana	Es el valor ubicado en el centro de un conjunto de datos ordenados.  Si el numero de datos es impar la mediana es exactamente el dato central. Si el número de datos es par, la mediana es el valor medio de los datos centrales y no es un dato de conjunto. Su sigla es : Me
Moda	Es el valor de la característica que mas se repite en una población o muestra. Su sigla es : Mo

REPRESENTACIÓN DE LOS DATOS OBTENIDOS EN GRÁFICOS ESTADÍSTICOS
Existe una gran cantidad de gráficos para la representación de datos estadísticos, entre los principales tenemos:
Gráficos de Barras	El gráfico de barras, como su nombre lo indica, está constituido por barras rectangulares de igual ancho, conservando la misma distancia de separación entre sí. Se utiliza básicamente para mostrar y comparar frecuencias de variables cuantitativas o comportamientos  en el tiempo, cuando el número de ítems es reducido.
Gráfico de sectores Circulares	Usualmente llamado gráfico de torta, debido a su forma característica de una circunferencia dividida en sectores, por medio de radios que dan la sensación de un pastel cortado en porciones. Se usa para representar variables cualitativas en porcentajes o cifras absolutas cuando el número de ítems no es superior a 5 y se quiere resaltar uno de ellos.
Gráfico de líneas o Tendencia	Usado básicamente para mostrar el comportamiento de una variable cuantitativa a través del tiempo. El gráfico de líneas consiste en segmentos rectilíneos unidos entre sí, los cuales resaltan las variaciones de la variable por unidad de tiempo.

¿QUÉ SON LOS PICTOGRAMAS?
Son representaciones visuales que registran información haciendo uso de figuras o dibujos.  El tamaño de las figuras está determinado por el número de veces que aparece el dato correspondiente.
Por ejemplo:
Juan Trabaja en una empresa de mensajería. Durante el mes de febrero registró el número de galones de gasolina que consumió su vehículo cada semana. Los resultados fueron:	Gasolina consumida en febrero Semana Consumo en galones Primera 108 Segunda 114 Tercera 84 Cuarta 147
Con la anterior información construyamos un pictograma que presente la información recolectada por Juan, de manera que cada dibujo represente 12 galones:

HORA DE PRACTICAR

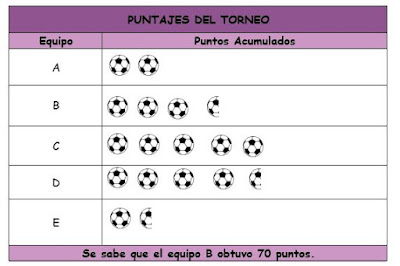
La siguiente figura muestra los puntajes de cinco equipos de futbol al finalizar un torneo.

 

Realice la tabla de frecuencias, halle la media aritmética, la mediana, la moda y realice gráficas de barras, de líneas y de torta.

Hacemos la tabla de frecuencias asi:

Frecuencia absoluta: la hallamos contando los balones que nos dieron en el pictograma para cada equipo.  Cada balón representa 20 puntos.

Frecuencia absoluta acumulada: tomamos la primera frecuencia absoluta 40  y empezamos a sumar la siguiente:

40 + 70= 110 para el equipo b

110+100=210 para el equipo c

Y así sucesivamente con todos los equipos.

Frecuencia relativa: tomamos los datos de la columna de la frecuencia absoluta y los dividimos por el numero de datos 330.

Equipo A:  40/330 = 0.12121212

Equipo B: 70/330= 0,212121

Equipo C: 100/330= 0,303030

HACEMOS LAS GRÁFICAS ASÍ:

Gráfica de barras:

Gráfica de líneas o Tendencia

Gráfica de sectores circulares:

HALLAMOS LAS MEDIDAS DE TENDENCIA CENTRAL:

 Déjame tus comentarios !